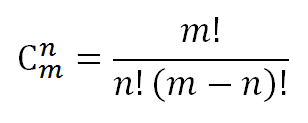概要
在做NOIP提高组day2第一题时,这个题的目标就是计算出组合数,也即题目中的系数。
实战
方法一
使用组合数公式
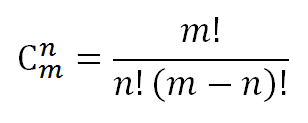
可以看到,里面是三个阶乘,按照这个思路,可以这样
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| #include<iostream>
using namespace std;
int factor(int n)
{
if (n==0|n==1)
return n;
return n*factor(n-1);
}
int main ()
{
int n,m,ans;
scanf("%d%d",&n,&m);
ans=factor(m)/(factor(n)*factor(m-n));
printf("%d",ans);
}
|
方法二
使用组合书递推公式
C(M-1,N-1)+C(M-1,N)=C(M,N)
下面是代码实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
| #include <iostream>
int aa[1000][1000];
using namespace std;
int conbinatorics(int n,int m)
{
if(aa[n][m])
return aa[n][m];
if(m==1)
{
return aa[n][m]=n;
}
if(n==m)
{
return aa[n][m]=1;
}
return aa[n][m]=conbinatorics(n-1,m-1)+conbinatorics(n-1,m);
}
int main()
{
int n,m;
cin>>n>>m;
cout <<conbinatorics(n,m)<< endl;
return 0;
}
|
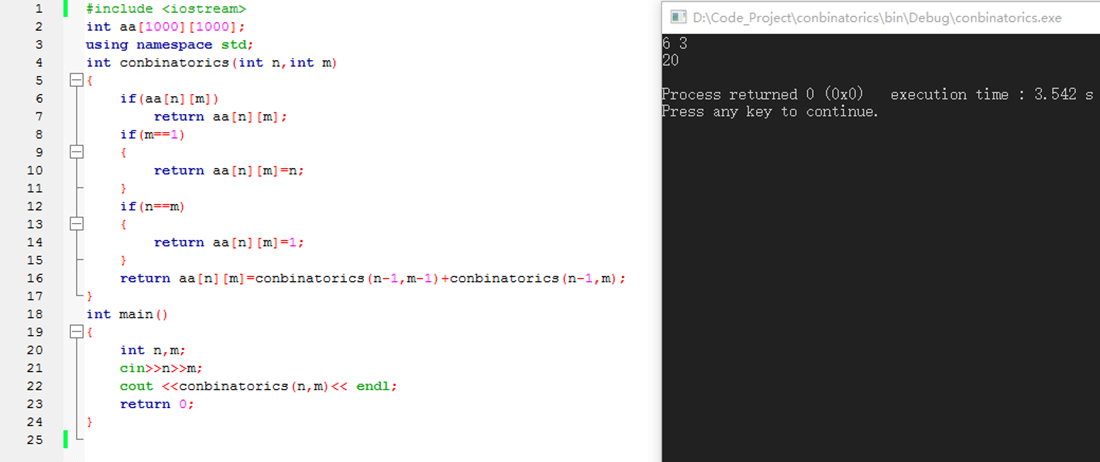
这里使用了动态规划————记录结果再利用,本可以节省很多时间,但是在这个代码示范中体现得不明显。请看下面。
斐波那契数列
F(1)=1,F(2)=1, F(n)=F(n-1)+F(n-2)
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| #include<iostream>
using namespace std;
int F(int n)
{
if(n==1||n==2)
return 1;
else
return F(n-1)+F(n-2);
}
int main ()
{
int n;
cin>>n;
cout<<F(n)<<endl;
return 0;
}
|
示例,当n= 40时,用时0.654s,
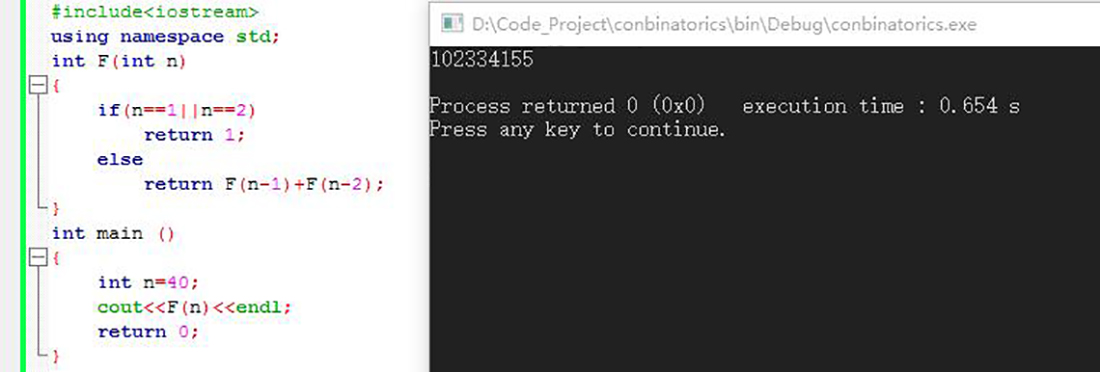
用动态规划,代码实现如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| #include<iostream>
using namespace std;
int array[1000];
int F(int n)
{
if(array[n])
return array[n];
else
{
array[n]=F(n-1)+F(n-2);
return array[n];
}
}
int main ()
{
int n=40;
array[2]=array[1]=1;
cout<<F(n)<<endl;
return 0;
}
|
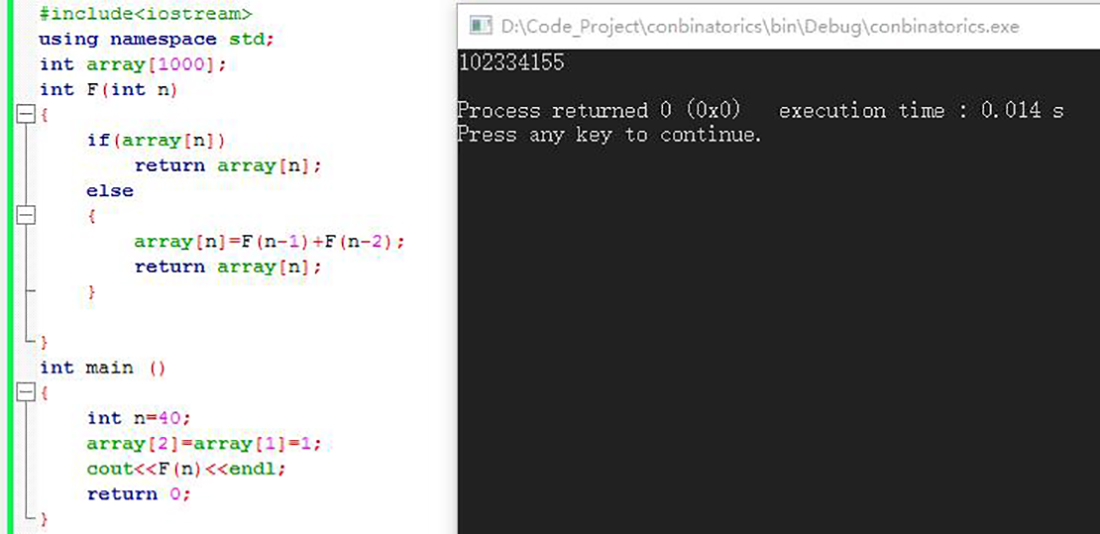
时间大幅度减少,虽然仍然不到一秒钟,但是用时相差约46倍,已经是巨大的差别了。
原因如下:
1
2
3
4
| F(40)=F(39)+F(38);
F(39)=F(38)+F(37);
F(38)=F(37)+F(36);
······
|
仔细一看,虽然算法没错,但是F(39)和F(38)被计算了两次,如果继续往下的话,会发现有许多数倍计算了很多次,那么在第一次用到这个数的时候,就把它所对应的结果记录在array中,需要用的时候直接用就好了,节省很多运行时间。
总结
动态规划————记录结果再利用
生命在于折腾